Análisis de la relación de factores SEO en R Studio
El mundo online no para de evolucionar y es innegable que las empresas se encuentran en un escenario cada vez más competitivo. Este escenario requiere de estrategias más solidas para conseguir los mejores resultados.
En Internet República trabajamos con clientes que acceden a un gran volumen de datos, y es necesario un tratamiento más técnico para convertir estos datos aislados en información relevante, y así mejorar el negocio online. En este sentido, el análisis estadístico nos puede ser de gran utilidad para el análisis masivo de datos y obtención de conclusiones empíricas.
Lo que pretendemos en el siguiente artículo es explicar cómo analizar la existencia de relación entre variables, utilizando el lenguaje de análisis estadístico R. Para ello, vamos a hacer uso de la correlación y regresión estadística.
La existencia de correlación o asociación entre 2 variables cuantitativas, viene determinada por la presencia de diferencias en las distribuciones condicionales de una variable para los distintos valores de la otra. En este caso nos vamos a ceñir al supuesto de un modelo de relación lineal.
Caso: ¿Qué podríamos decir de la asociación entre el tráfico estimado de un sitio y el número de backlinks que apuntan a este?
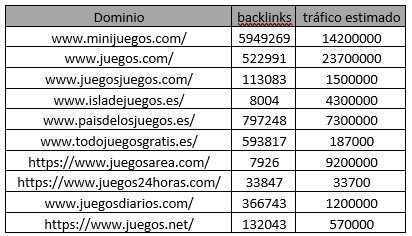
Nuestro objetivo es determinar el tráfico de un sitio a partir del número de enlaces entrantes, y para ello hemos analizado los principales competidores de “juegos gratis online” y hemos extraído con la herramienta aHrefs el tráfico estimado al dominio y el número de backlinks que apuntan a éste. Estos son los datos con los que hemos trabajado:
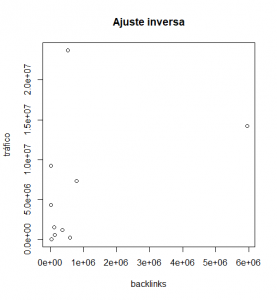
Para representar el diagrama de dispersión de las dos variables y determinar si la relación entre ambas variables es lineal, y por lo tanto, tiene sentido aplicar un modelo de regresión lineal simple, podemos hacer uso de la función plot:
> plot(datos$backlinks,datos$trafico, xlab='backlinks',ylab='tráfico')
Este es el resultado:
A simple vista con este gráfico podríamos determinar si existe cierto grado de relación entre varias variables. En nuestro caso, la muestra es muy pequeña y no podemos verlo tan claro, aún así, procedemos al ajuste del modelo lineal:
> regresion <- lm(datos$trafico ~ datos$backlinks, data = datos) > regresion Coefficients: (Intercept) backlinks 4.760e+06 1.711e+00
Teniendo en cuenta la salida, el modelo lineal podría escribirse de la siguiente forma:
Visitas i= 4760000 + 1711 backlinks i
Podemos obtener más información sobre el modelo de regresión que hemos calculado aplicando la función summary:
> summary(regresion) Residuals: Min 1Q Median 3Q Max -5589341 -4358939 -2097865 763185 18044878 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 4.760e+06 2.649e+06 1.797 0.11 datos$backlinks 1.711e+00 1.380e+00 1.240 0.25 Residual standard error: 7504000 on 8 degrees of freedom Multiple R-squared: 0.1612, Adjusted R-squared: 0.05635 F-statistic: 1.537 on 1 and 8 DF, p-value: 0.2501
En la tabla coefficients, podemos ver como cada parámetro viene acompañado del valor de un estadístico t de Student y un p-valor que sirven para determinar si los efectos de la variable independiente son importantes. Como el p-valor de ambos parámetros es mayor de 0,05, podemos pensar que los cambios en los parámetros no están asociados con cambios en la variable dependiente.
Finalmente, encontramos el valor de Multiple R-squared y Adjusted R-squared, que nos indican si existe un buen ajuste del modelo lineal a los datos. En nuestro caso, ambos valores son próximos a 0, por lo que el modelo lineal no se ajusta de forma aceptable a nuestros datos.
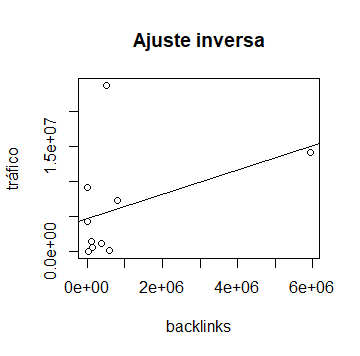
R y RStudio nos permiten dibujar la recta de regresión lineal sobre el diagrama de dispersión, para visualizar la distancia entre los valores observados y los que el modelo pronostica. Para ello, hacemos uso de la siguiente orden:
> abline(regresion)
El principal objetivo de la regresión es encontrar la función que mejor explique la relación entre la variable dependiente e independiente. Pero, aunque la regresión garantiza que el modelo construido es el mejor posible, puede que, aún así, no sea un buen modelo para hacer predicciones por la falta de relación de ese tipo entre las variables. De manera que, para validar el modelo, es necesario medidas que nos digan el grado de dependencia entre las variables. En este caso, podemos recurrir al coeficiente de correlación lineal de Pearson para la relación lineal entre variables.
Cuanto más próximo esté a 1, mejor será el modelo de regresión. En R o RStudio podemos calcularlo utilizando la función cor:
> cor(datos$backlinks,datos$trafico) [1] 0.4014979
El resultado lo podríamos interpretar de la siguiente forma:
El 40,10% del tráfico a un sitio es explicado por el número de backlinks.
Conclusión
Podemos concluir que el modelo calculado no describe el comportamiento del tráfico dado los valores de la otra variable (backlinks). Por desgracia, cuando se trata de estudiar la influencia de variables en posicionamiento de un sitio web en los buscadores, no se trata de un modelo lineal simple ni de dos variables, sino que nos enfrentamos a funciones mucho más complejas en las que se estudian más factores, pero en el caso de conseguir un modelo adecuado, podríamos predecir cosas tan interesantes como los niveles de tráfico que obtendríamos para un cierto valor de backlinks o de cualquier otra variable que se estudiara.
Finalmente, hay que tener en cuenta que la fiabilidad de las predicciones que hagamos con un modelo de regresión depende, además, de cosas como el coeficiente de determinación o la variabilidad de la población del tamaño muestral: cuanto mayor sea, más información tendremos y, en consecuencia, más fiables serán las predicciones.
Además, hay que tener en cuenta que un modelo de regresión es válido para el rango de valores observados en la muestra, pero fuera de ese rango no tenemos información del tipo de relación entre las variables, por lo que no deberíamos hacer predicciones para valores que estén lejos de los observados en la muestra.